
題目列表(包括答案和解析)
| 時間t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日銷售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
| 1 |
| 4 |
| 時間t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日銷售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
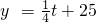 (1≤t≤20且t為整數(shù)).下面我們就來研究銷售這種商品的有關問題:
(1≤t≤20且t為整數(shù)).下面我們就來研究銷售這種商品的有關問題:| 時間t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日銷售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
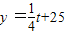 (1≤t≤20且t為整數(shù)).下面我們就來研究銷售這種商品的有關問題:
(1≤t≤20且t為整數(shù)).下面我們就來研究銷售這種商品的有關問題:湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com