
�}Ŀ�б�(�����𰸺ͽ���)
��֪�ɂ�(g��)�������FP-ABCD�cQ-ABCD�ĸ߷քe��1��2,AB=4.

(��)�C��PQ��ƽ��ABCD;
(��)����ֱ��AQ�cPB���ɵĽ�;
(��)���c(di��n)P��ƽ��QAD�ľ��x.
��֪�ɂ�(g��)�������FP-ABCD�cQ-ABCD�ĸ߷քe��1��2,AB=4.
(��)�C��PQ��ƽ��ABCD;
(��)����ֱ��AQ�cPB���ɵĽ�;
(��)���c(di��n)P��ƽ��QAD�ľ��x.
��֪�ɂ�(g��)�������FP-ABCD�cQ-ABCD�ĸ߷քe��1��2, AB=4
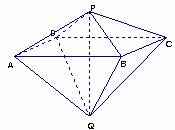 (��) �C��:PQ
(��) �C��:PQ![]() ƽ��ABCD ;
ƽ��ABCD ;
(��) ����ֱ��AQ�cPQ���ɵĽ�;
(��) ���c(di��n)P��ƽ��QAD�ľ��x.

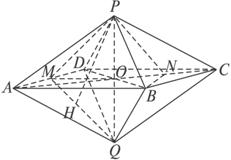
(1)�C��PQ��ƽ��ABCD;
(2)����ֱ��AQ�cPB���ɵĽ�;
(3)���c(di��n)P��ƽ��QAD�ľ��x.
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com