【答案】
(1)解:設(shè)Q(x0����,4)��,代入y2=2px得x0= 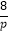 ���,
���,
∴|PQ|= 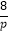 ���,|QF|=
���,|QF|=  +x0=
+x0=  +
+ 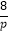 .
.
由題設(shè)得  +
+  =2×
=2×  ,解得p=﹣4(舍去)或p=4��,
,解得p=﹣4(舍去)或p=4��,
∴拋物線C的方程為y2=8x.
(2)解:由題設(shè)知���,l與坐標(biāo)軸不垂直��,且過焦點(diǎn)F(2�,0),
故可設(shè)l的方程為x=my+2(m≠0)�����,
代入y2=8x得y2﹣8my﹣16=0.
設(shè)A(x1����,y1),B(x2�,y2),則y1+y2=8m�,y1y2=﹣16.
故AB的中點(diǎn)為D(4m2+2,4m)����,
|AB|= 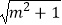 |y1﹣y2|=
|y1﹣y2|= 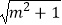
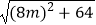 =8(m2+1).
=8(m2+1).
又l′⊥l�����,所以l′的斜率為﹣m�����,
所以l′的方程為x=﹣  y+4m2+6.
y+4m2+6.
將上式代入y2=8x�����,并整理得y2+  y﹣8(4m2+6)=0,
y﹣8(4m2+6)=0,
設(shè)M(x3�����,y3)��,N(x4���,y4)���,
則y3+y4=﹣  ,y3y4=﹣8(4m2+6).
,y3y4=﹣8(4m2+6).
故MN的中點(diǎn)為E( 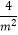 +4m2+6�����,﹣
+4m2+6�����,﹣  )����,
)����,
|MN|= 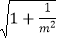 |y3﹣y4|=
|y3﹣y4|= 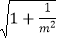
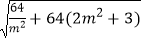 =
= 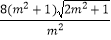 ,
,
由于MN垂直平分AB�,故A,M,B���,N四點(diǎn)在同一圓上等價于|AE|=|BE|=  |MN|�����,
|MN|�����,
又在Rt△ADE中�����,丨AD丨2+丨DE丨2=丨AE丨2�����,
從而  |AB|2+|DE|2=
|AB|2+|DE|2=  |MN|2�,
|MN|2�,
即16(m2+1)2+(4m+  )2+(
)2+( 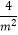 +4)2=
+4)2= 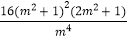 ���,
���,
化簡得m2﹣1=0,m=±1���,
所以當(dāng)A���,M,B,N四點(diǎn)在同一圓上時���,l的方程為x=±y+2��,即x±y﹣2=0.
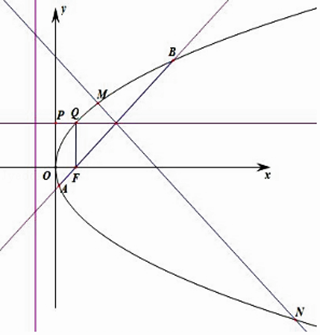
【解析】(1)將Q(x0��,4)代入拋物線方程�����,求得丨PQ丨��,根據(jù)拋物線的定義�,即可求得p的值���,求得C的方程�;(2)設(shè)l的方程為 x=my+1 (m≠0)����,代入拋物線方程化簡,利用韋達(dá)定理���、中點(diǎn)公式�����、弦長公式求得弦長|AB|.把直線l′的方程代入拋物線方程化簡���,利用韋達(dá)定理�����、弦長公式求得|MN|.由于MN垂直平分線段AB��,故AMBN四點(diǎn)共圓等價于|AE|=|BE|=  |MN|���,由此求得m的值,可得直線l的方程.
|MN|���,由此求得m的值,可得直線l的方程.