
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:填空題

查看答案和解析>>
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:填空題
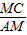 的值是 .
的值是 .查看答案和解析>>
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:填空題
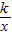 的交點A的橫坐標是1,則關(guān)于x的不等式
的交點A的橫坐標是1,則關(guān)于x的不等式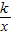 +x2+1<0的解集是 .
+x2+1<0的解集是 .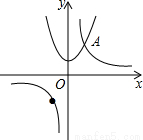
查看答案和解析>>
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:解答題
查看答案和解析>>
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:解答題

查看答案和解析>>
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:解答題

查看答案和解析>>
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:解答題
| 組別 | 成績(分) | 頻數(shù) |
| A | 50≤x<60 | 3 |
| B | 60≤x<70 | m |
| C | 70≤x<80 | 10 |
| D | 80≤x<90 | n |
| E | 90≤x<100 | 15 |

查看答案和解析>>
科目: 來源:2012年浙江省杭州市中考數(shù)學模擬試卷(33)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com